Voxel Continuity Algorithm
Besides performance optimization, there are still things to do to enhance the voxel engine. One thing that voxel engines rarely do (though voxel farm does) is identify any structures that are not attached to the main structure and break them off into their own coordinate system so that they can obey a physics engine and fall. Having multiple coordinate systems is no problem at all- each coordinate system has a separate octree and a transform matrix. The real challenge is identifying disconnected volumes.
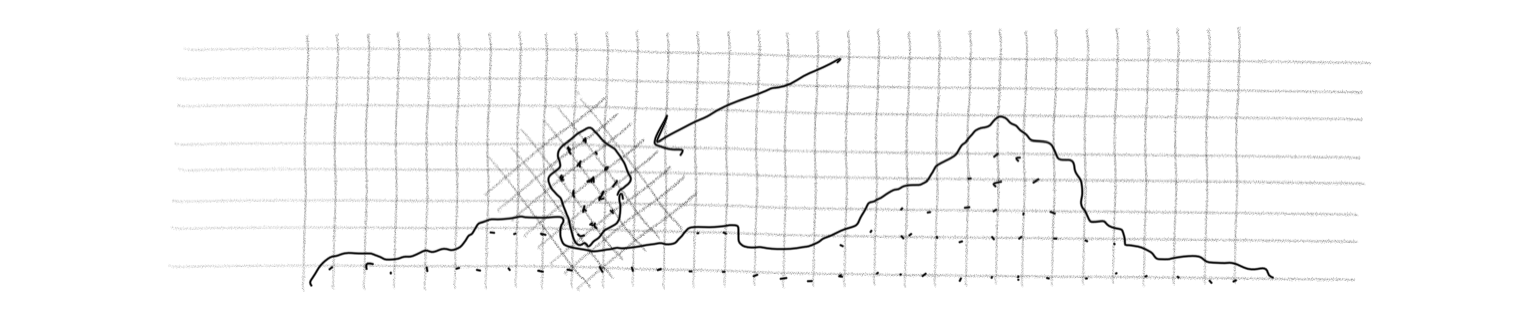
The naive solution would be to attempt to pathfind from some point to each other solid voxel, which isn’t a viable solution because it would take forever.

For the vast majority of cases, the octree structure can provide a crucial advantage. First, information about connectivity must be calculated and stored in a bitmask on each branch. This information would include whether the branch contains solid mass and whether that mass is contiguous to the mass of the branches neighboring it in each direction. The calculation is recursive, simple, and fast.
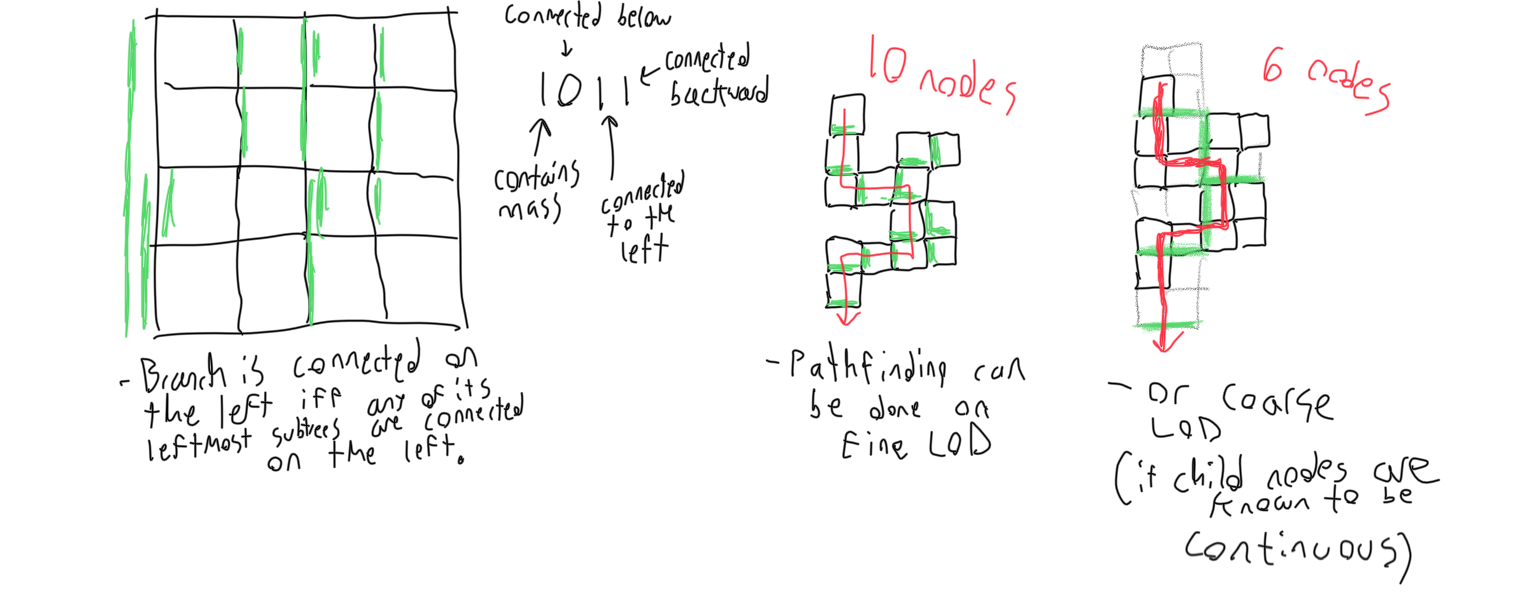
Next, the octree is recursively checked for continuity with the following rules: First, check all subtrees for continuity with the recursive step. After this, it can be assumed that all subtrees will be continuous, because if and when any children fail, a piece of the octree will break off into its own coordinate system, and its parent (this node) will be recalculated. Next, see if the eight subtrees are continuous to each other, without considering any neighbors besides the eight. If they are, the test is passed. If they cannot be proven to be continuous or discontinuous without considering neighboring cells, the tree and its depth are added to a registry.
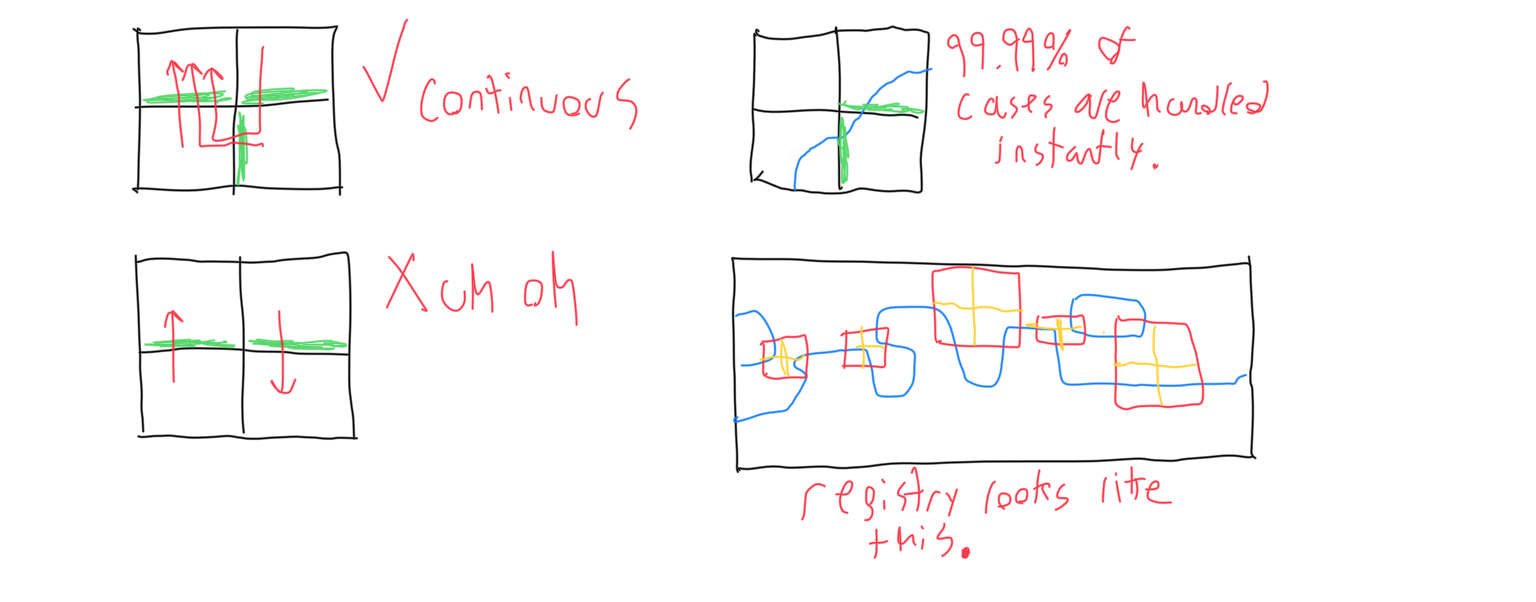
Outside of the recursion, consider each tree in the registry, smallest depth first. Using a symmetric A* algorithm, the program attempts to pathfind through neighboring cells of the same depth to test continuity.
-
If a path is found, the tree is removed from the registry.
-
If the A* algorithm runs out of open nodes, the side that ran out of open nodes must separate into a new coordinate system, and that tree’s parent node is added to the registry.
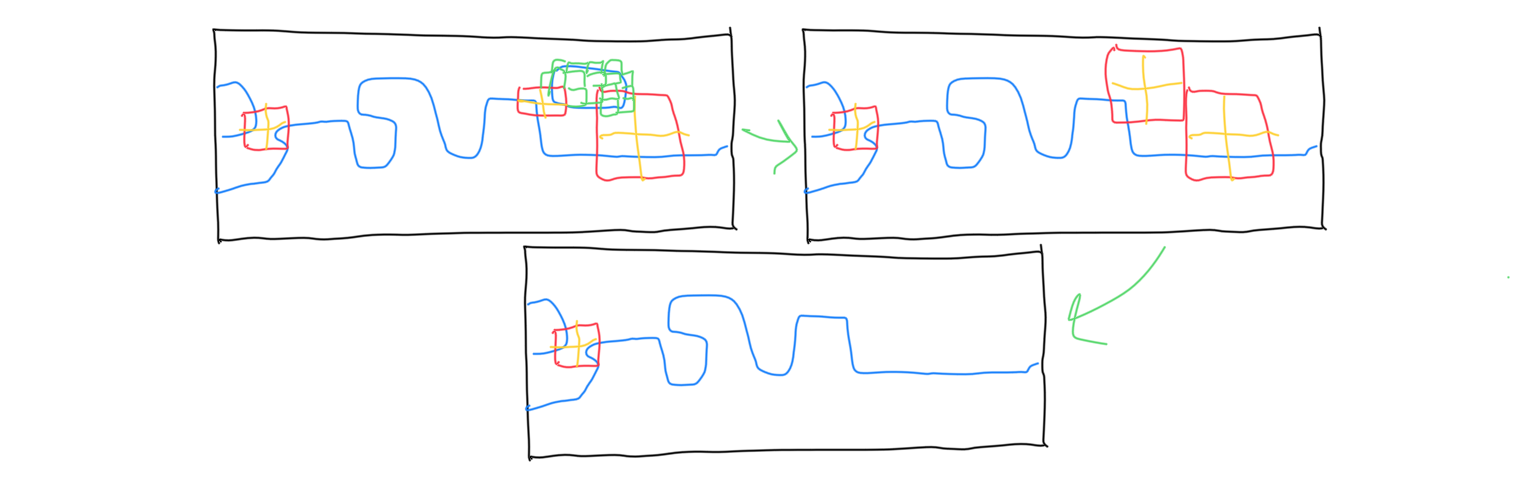
-
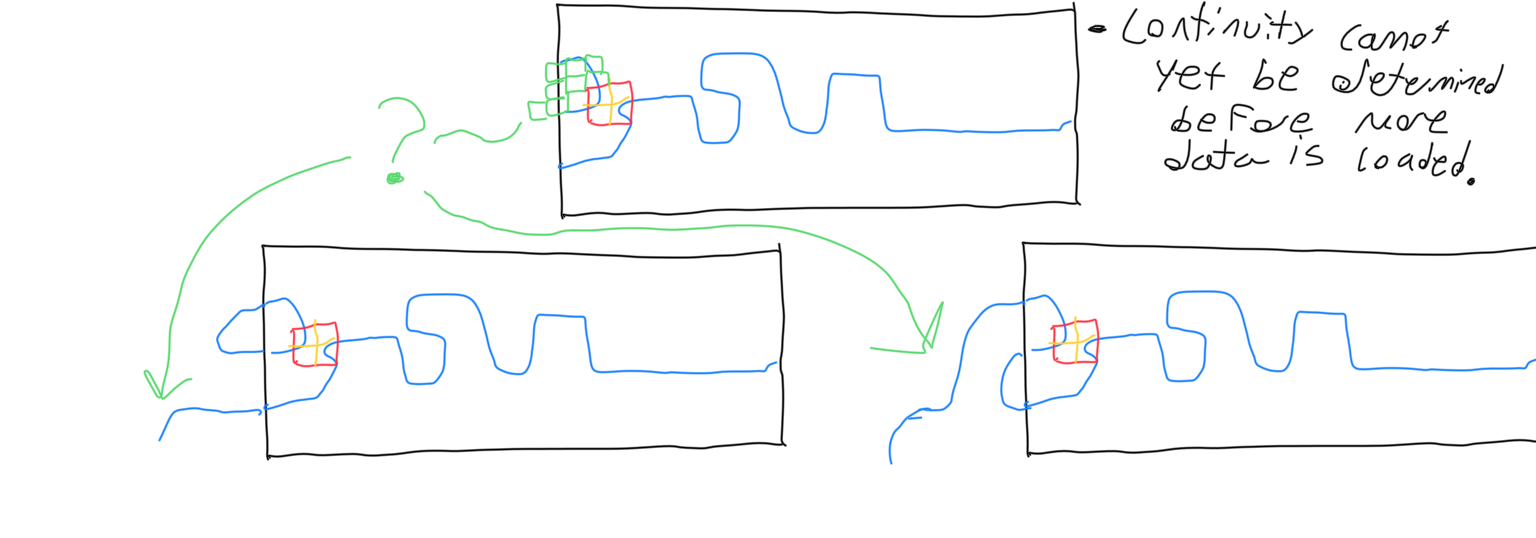
If the A* algorithm attempts to add a cell that is in an unloaded chunk or in the registry to the open list, then the search is stopped and the node remains in the registry, for the program has not loaded enough data to determine continuity yet. The registry is revisited anytime a chunk loads in or when a chunk is checked for disconnected volumes.
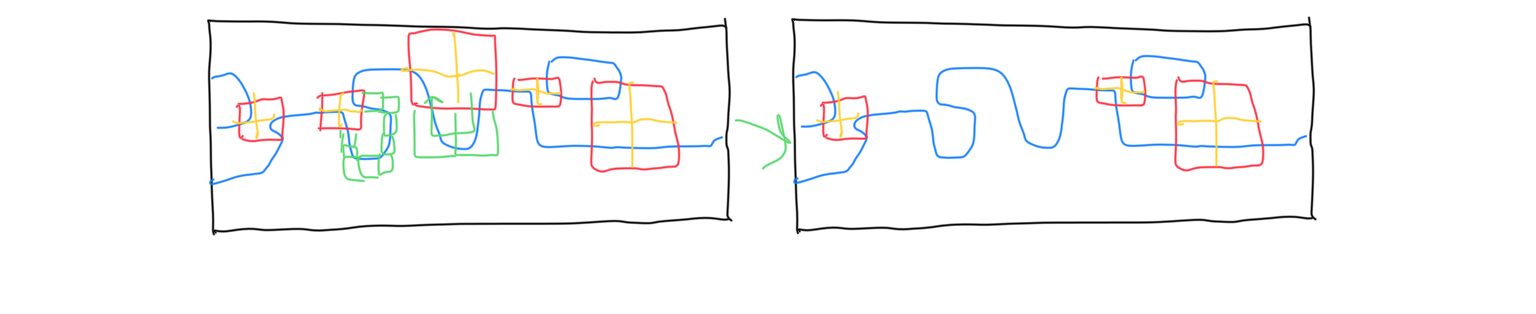
This approach is extremely efficient for a number of reasons. First, it naturally filters out the ‘easy cases’ before they even get to the registry. Easy cases are the ones where the subtrees are continuous without needing to consider neighboring cells. Almost all cases are easy cases, so it’s good that they can be handled with just a handful of bitwise operations. Second, path finding can be done at a higher level than on a block-per-block basis. This figure demonstrates what I mean and the difference this can make. Third, even when all else fails, symmetric A* is able to finish very fast for this use case.
This algorithm also has very natural tie-ins for the rest of the game. Detecting when trees should stay in the registry until chunks load in is an enormous luxury, because it vastly reduces the number of paranoid recalculation that would have to be done if the program could not make this distinction. Also, when the symmetric A* runs out of open nodes and a floating island is identified, the closed list can be used as an exact itinerary for what parts of the octree must be replaced with air and moved into their own octree. The whole strategy is a great example of elegance in programming.