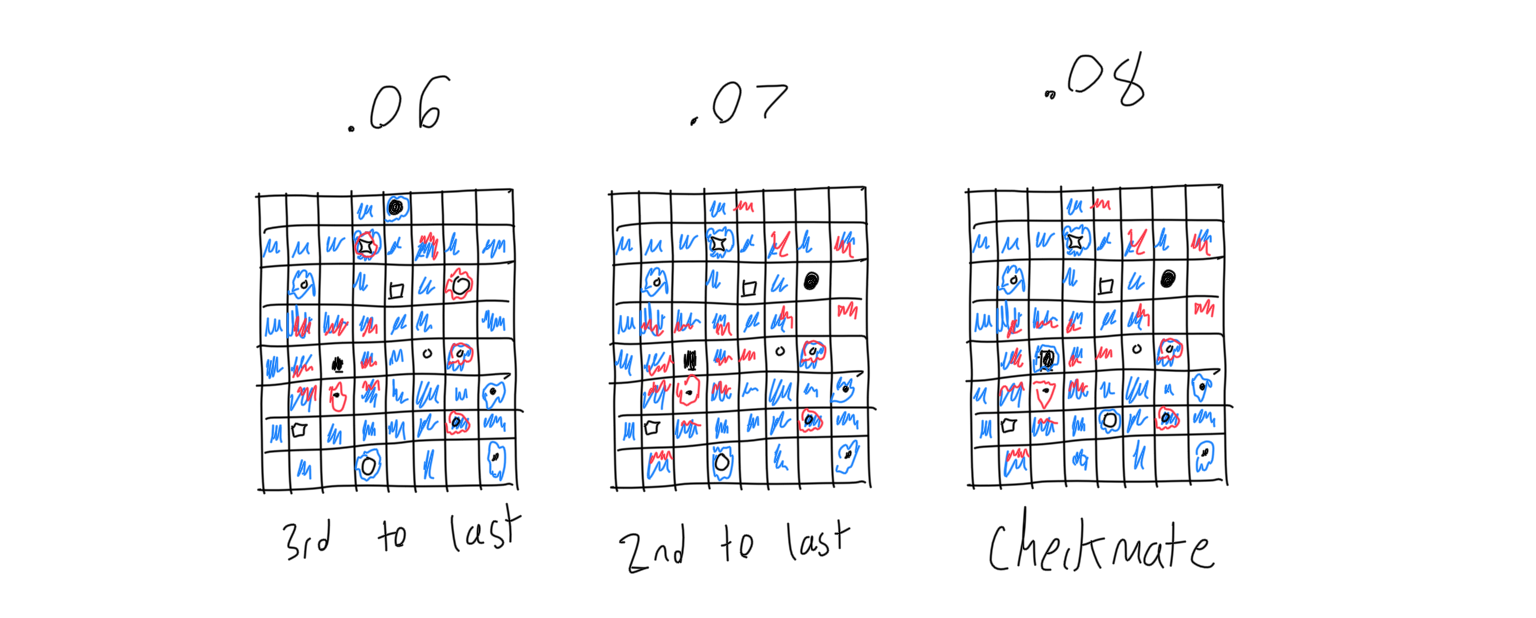Minmax trees
The other component to the chess AI is a minmax tree. This is what allows the program to look ahead to see which moves put it in a better position. When the program looks ahead some number of moves in advance, it constructs a tree that represents the next possible moves. After a certain number of moves in the future, the program will cap the tree off with the heuristic value of that node. It is assumed that the program will choose the best possible path for it, and the opponent will choose the worst path for the program. The heuristic for each node that is not a terminal node will be the max or min of its children respectively.
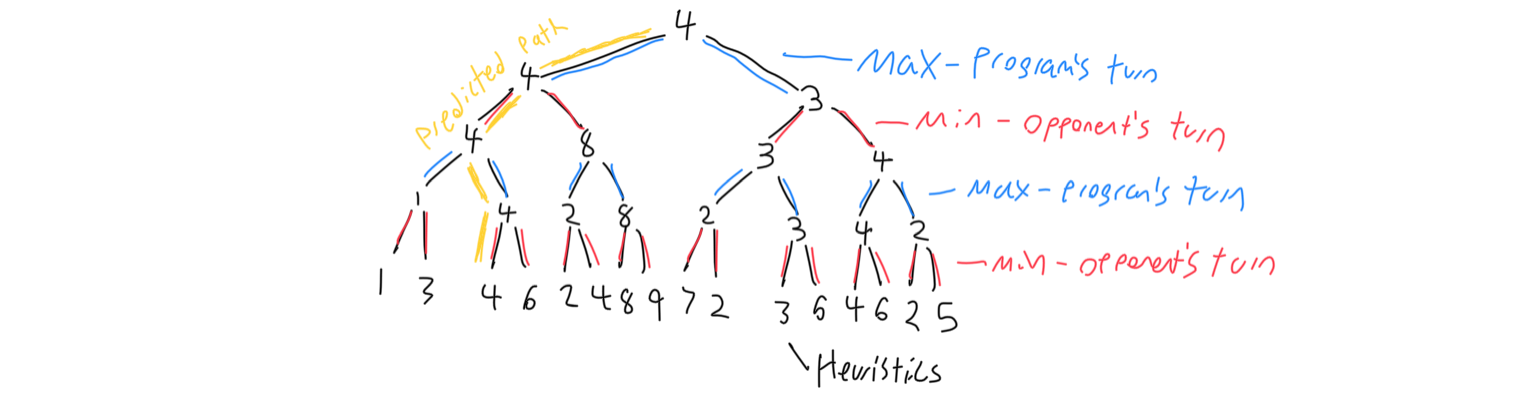
Consider the below diagram, where the tree is in the middle of being calculated. One of the paths does not need to be explored, because the only effect it could have on the value of its parent heuristic is to lower it, and its parent’s heuristic is already too low to be considered. It can be skipped. This process is known as alpha-beta pruning, and it eliminates a lot of computation needed, which allows the program to look further ahead. In general, anytime the maximum score that the minimizing player is assured of is greater than or equal to the minimum score that the maximizing player is assured of, that node does not need to be explored.
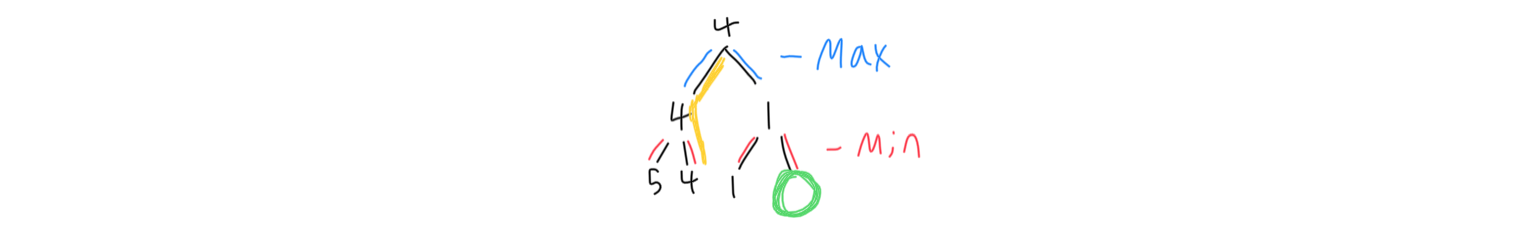
Each heuristic is expensive to calculate because it involves evaluating a neural network over the chess board. I had to play around with what inputs the neural network received to make it as effective as possible. I started with simply giving each square of the board an input for each piece it could possibly have. This was not feasible because of the number of nodes needed.

The second method I tried was using a convolutional neural network. A convolutional neural network re-uses groups of weights in a moving window over the input, which must be arranged in a grid.
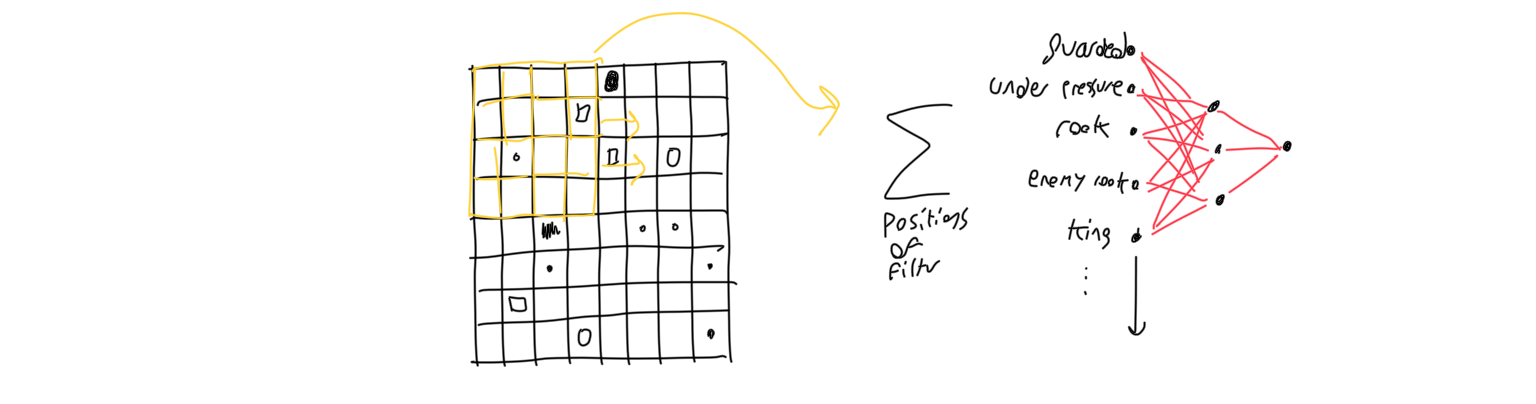
After experimenting with various convolution sizes and approaches, the best solution turned out to be adding another input to the neural network for which pieces were under pressure, or resting on a space that could be attacked by one of the opponents pieces. After that, smaller convolutions were much more effective because they trained faster and executed faster, allowing the program to look further ahead. The solution that reigned supreme was to use a neural network with an input for each kind of piece that could lie on that space, an input for if that space was under pressure, and an input for if that space were guarded. The neural network is evaluated for each square in the grid, and summed up to get the heuristic of the entire grid.
Once a game has completed, the neural network is trained over the last 8 games. The last game has the highest learning rate, with the learning rate tapering off by the 8th to last game, because it is easiest to determine a game’s outcome by later board positions. The program was trained by both playing against itself and also from games collected with a webscraper.