Neural networks
Stochastic gradient descent refers to making a function more accurate by adjusting its weights according to the derivative of the function’s error with respect to each weight.
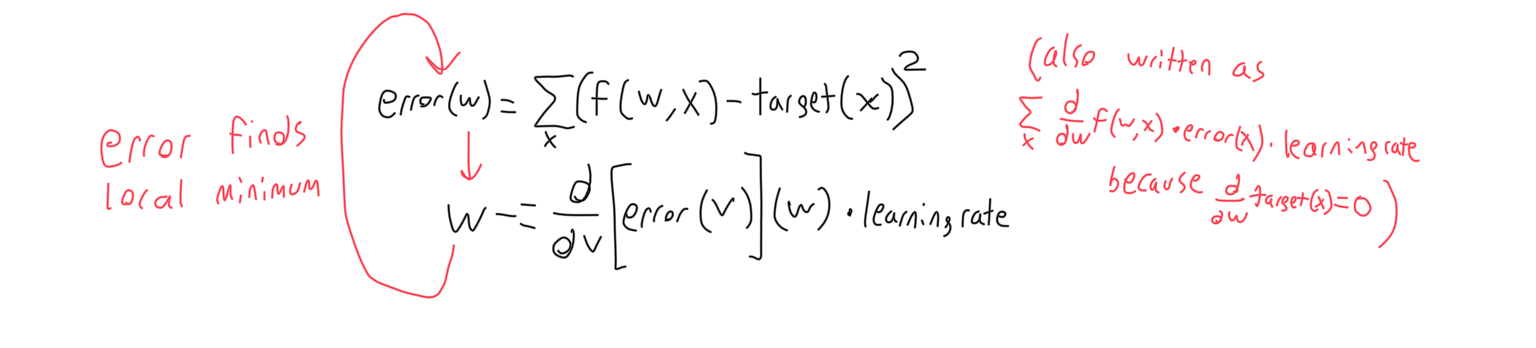
The more weights the function has, the more flexible the function can be. A good way to make a function with a lot of weights that can be executed quickly is to arrange the weights as a series of matrix transformations.

The resulting function will always be a linear model, which is very limited and could be solved with a linear regression method anyway. The solution is to apply a non-linear function to each vector in between matrices. This non-linear function is called an activation function. Many different activation functions are used, such as inverse tangent or a logistic function. The shape of the function is more important than its value.
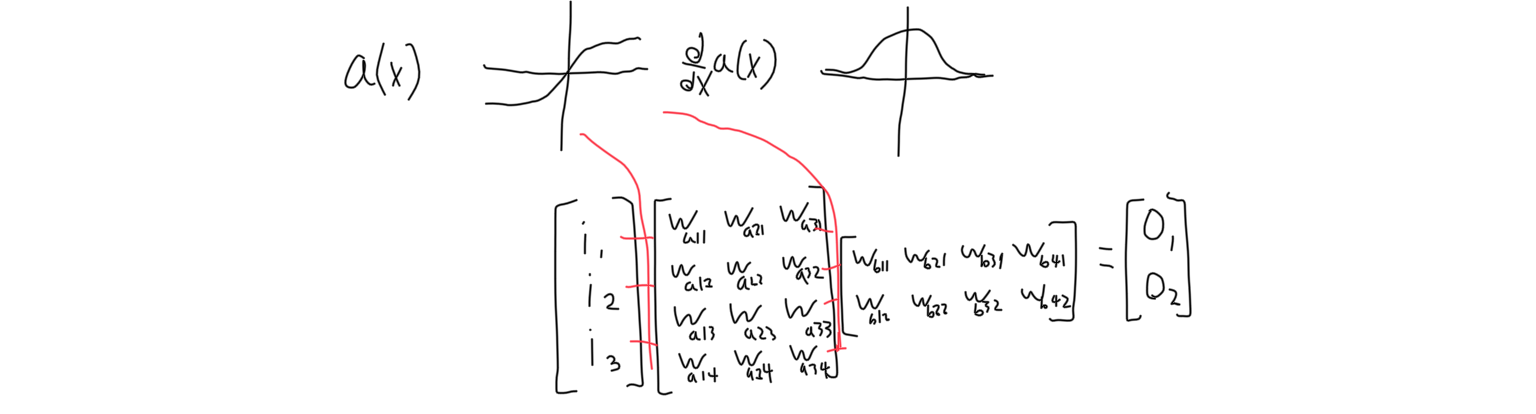
The above steps result in a neural network. It’s important to note that the most important parts of a neural network are not biomimetic. In my TED talk I liken the neural network to the way humans learn because it’s a good analogy, but the similarities aren’t the reason neural networks are able to work effectively. They work effectively because of the reasons stated above.