Understanding Rubik's Puzzles
In order to build an expressive and powerful simulator, the components that differentiate twisting puzzles must be understood. First of all, puzzles are usually regular polyhedra. Puzzles that are spherical or especially irregular are outside the scope of this simulator.

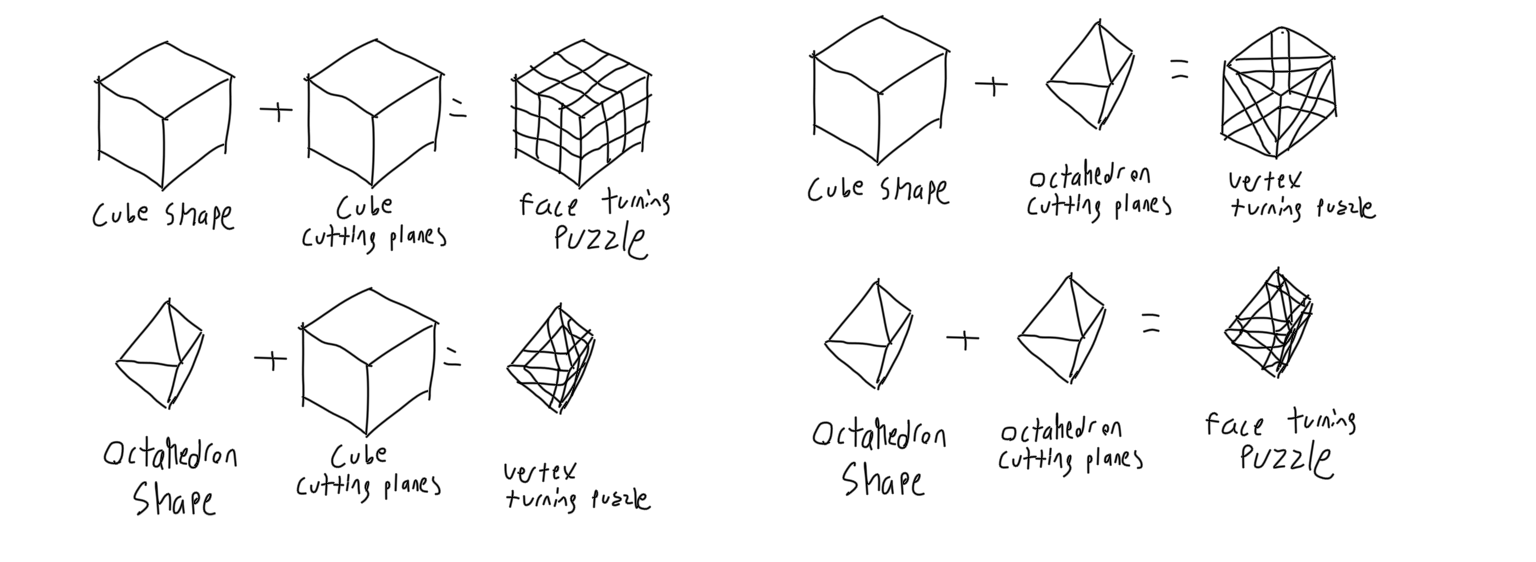
Secondly, puzzles are typically either face-turning, edge-turning, or vertex-turning. The simulator will support each of these (and a few more for technical reasons).




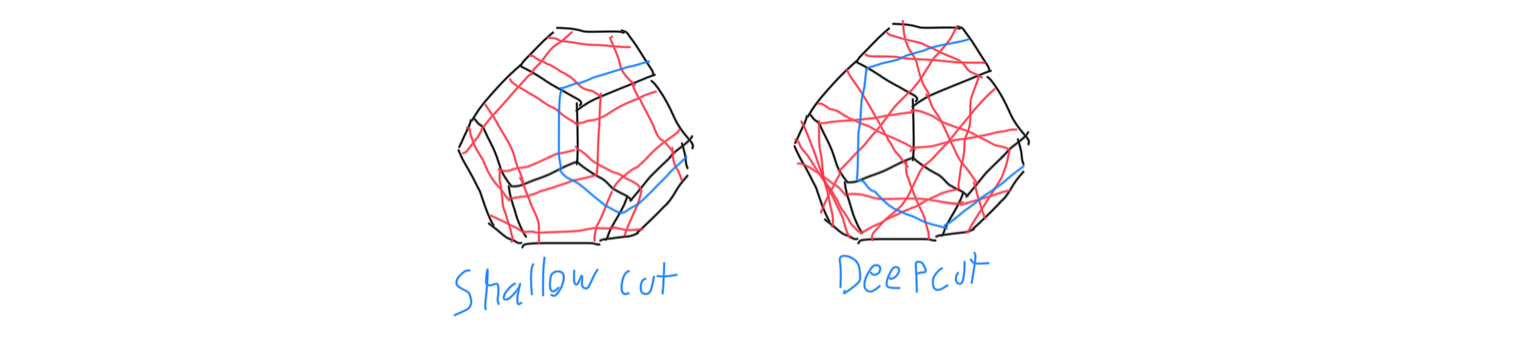
Third, some puzzles are ‘deep cut’ and some are ‘shallow cut’. Each face, edge, or vertex that can be twisted has a ‘cutting plane’, or a plane that divides the puzzle into a turning and not-turning region. Increasing the depth of the cutting plane on the puzzle often increases the challenge because deeper cuts produce pieces that can be moved by many different turns. Also, puzzles can be ‘high order’, which means they have multiple parallel cutting planes, such as a 4x4 or 5x5 rubik’s cube as opposed to a 3x3 rubik’s cube.


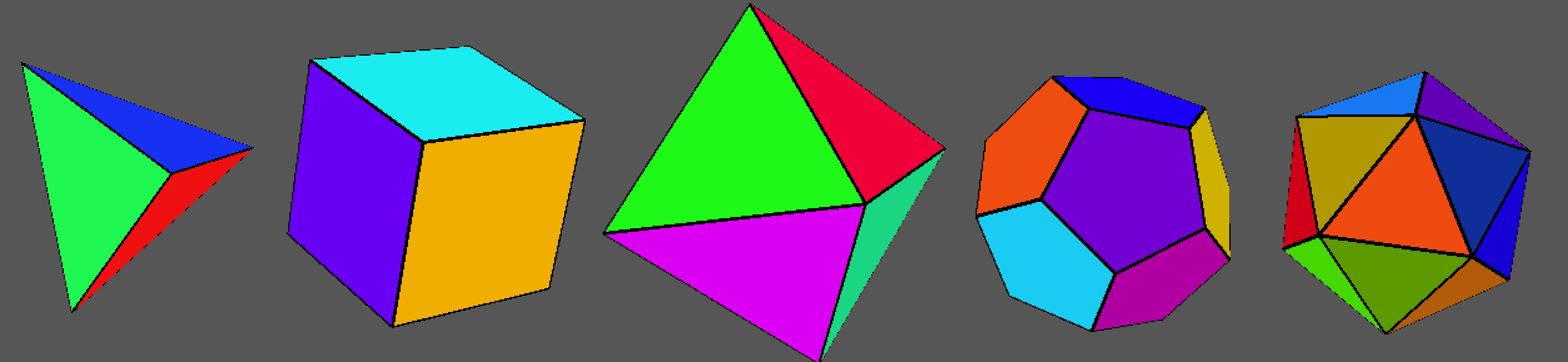
Simple puzzles can be defined by their cutting planes and planes that define their shape. A valid set of planes can be uniquely identified by a given set of normal vectors and a scalar depth. The set of normal vectors comes from a solid such as a dodecahedron, octahedron, etc. Sets of planes serve one of two distinct purposes. The volume of the puzzle is bounded by the shape planes, and cut into movable pieces by the cutting planes. Because pieces need to fit into their ending locations after a turn, they can only be rotated around symmetry groups of the solid they belong to. Therefore, cutting planes are always distributed along a symmetry group of the starting solid, with a given depth. Planes that define shape must also have the same symmetry group so that the puzzle does not change shape after it is turned. If a puzzle defined with some polyhedron’s shape planes is face turning, the cutting planes will be parallel to that shape’s faces. If the puzzle is vertex turning, the cutting planes will be parallel to that shape’s dual solid’s faces.

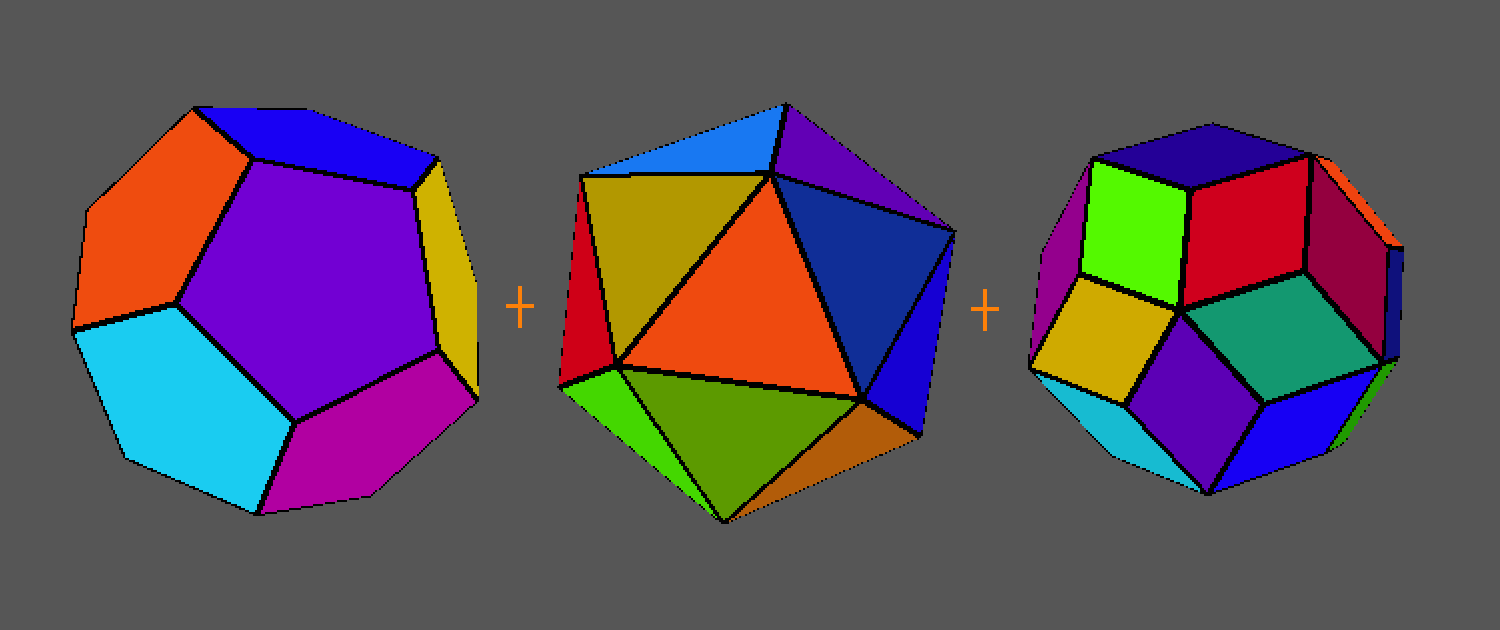
For a puzzle with edge turning, though, calculating the cutting planes can become more difficult. Knowing that a solid and its dual have the same edge-turning cutting planes, aligning the two solids allows a third to be generated. The third solid is the convex hull of the first two solid’s vertices, and its faces are perpendicular to the cutting planes of either edge turning puzzle.



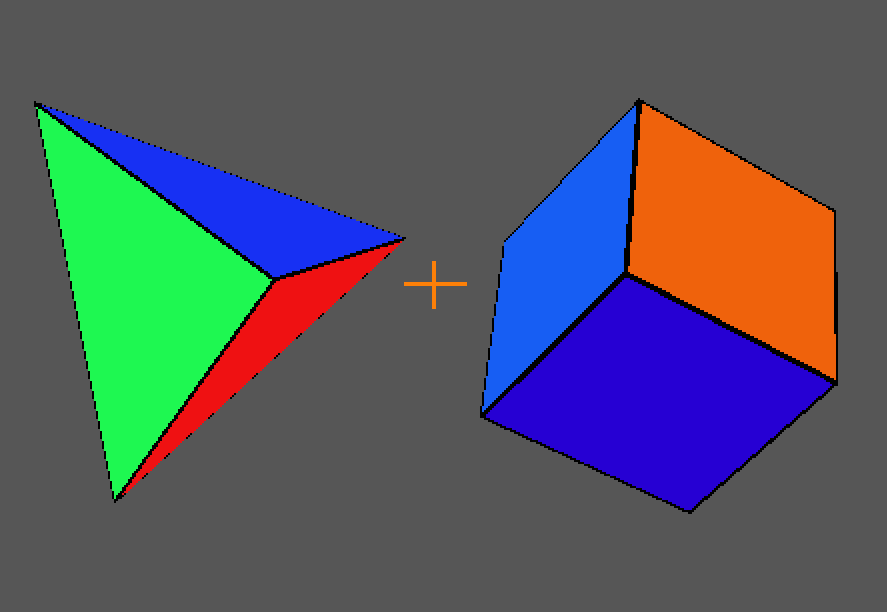

For cubes and octahedrons, the same process produces a different shape, the rhombic dodecahedron. The second set of symmetry groups consists of the cutting planes perpendicular to the faces of a cube (90 degree rotations), the faces of an octahedron (120 degree rotations), and the faces of a rhombic dodecahedron (180 degree rotations).


The final set of symmetry groups comes from the icosahedron (120 degree), dodecahedron (72 degree), and rhombic triacontahedron (180 degree) via the same process.