Proof engine operations
The proof algorithm involves performing a process similar to algebra, but with judgmental equality. When this kind of algebra is done, an object is created to store all restrictions placed on the unknown variables. The object stores the scope, which contains a reference to the signatures of all axioms usable by the machine in the first row, and the signatures of each unknown variable in the second. The object also stores some number of pairs of statements known to be judgmentally equal. Each pair of statements also has a scope associated with it for variables that are neither axioms nor unknown variables but are present in that pair of statements. I call the object a binding object, because it binds statements together so that they must be judgmentally equivalent.
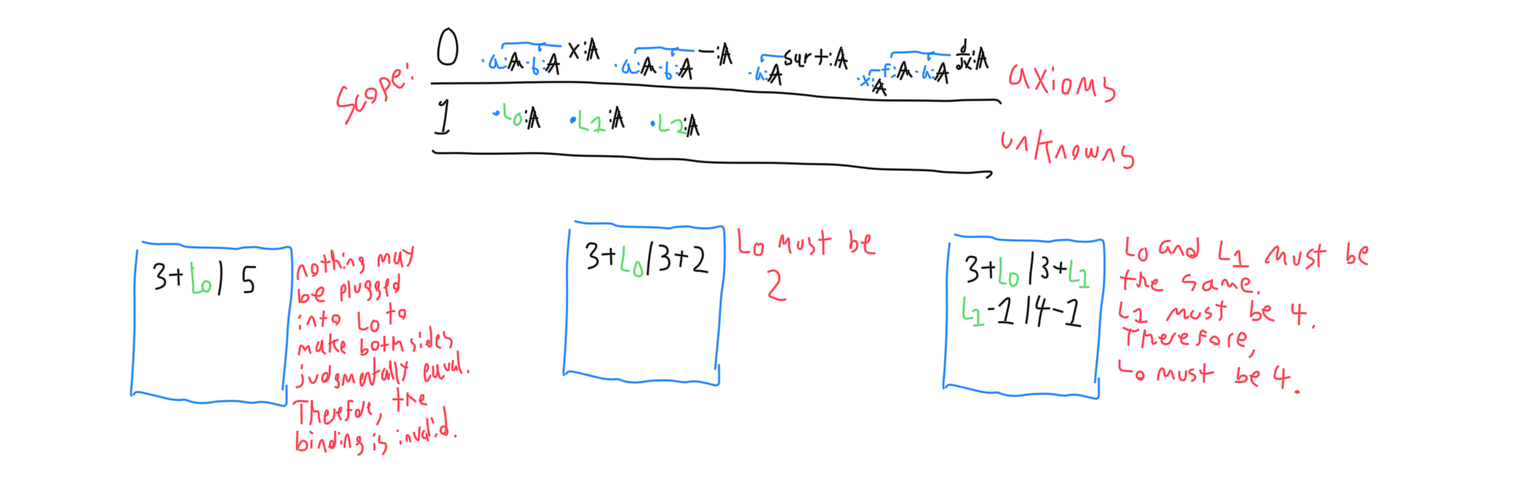
Simplifying binding objects provides information about the unknown variables that it operates on. The proof deducer is interested in simplifying binding objects until no more information can be extracted from them. The most basic form of simplification is recursively comparing both sides of each pair- if the two root nodes differ- either one of the root nodes is an unknown variable or there is no solution to the binding object and it must be destroyed. This often results in variables being created in the pair’s scope. After this process, all pairs consist of at least one structure whose root node is an unknown variable.
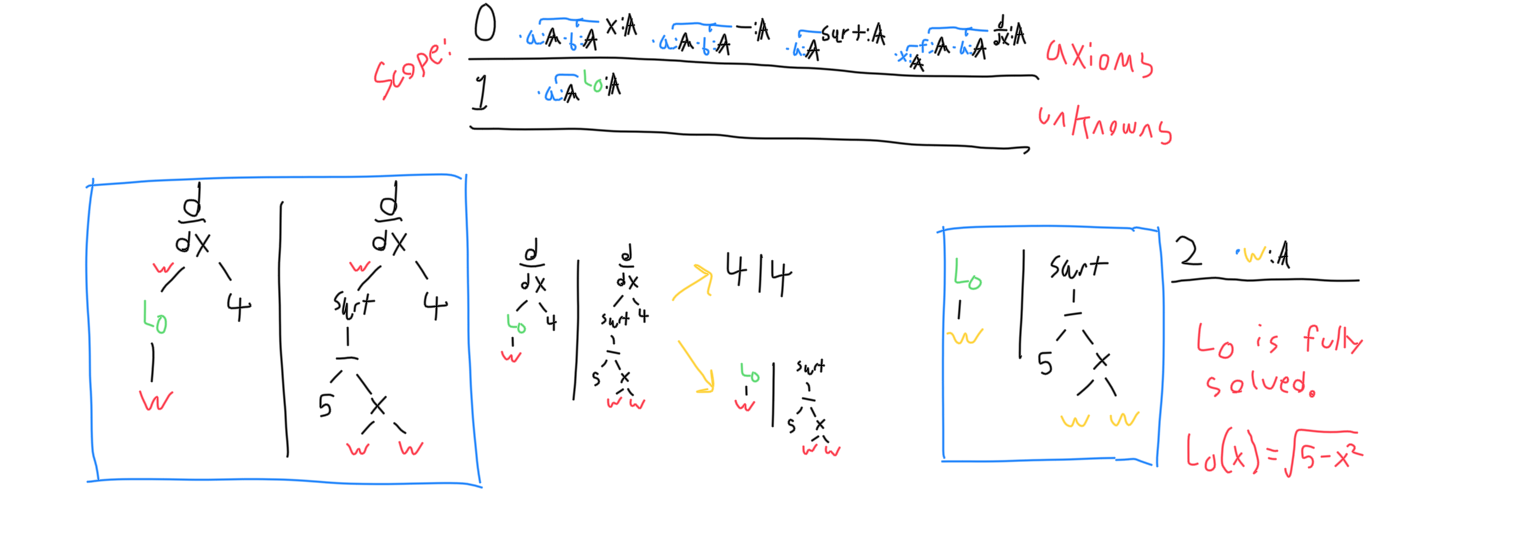
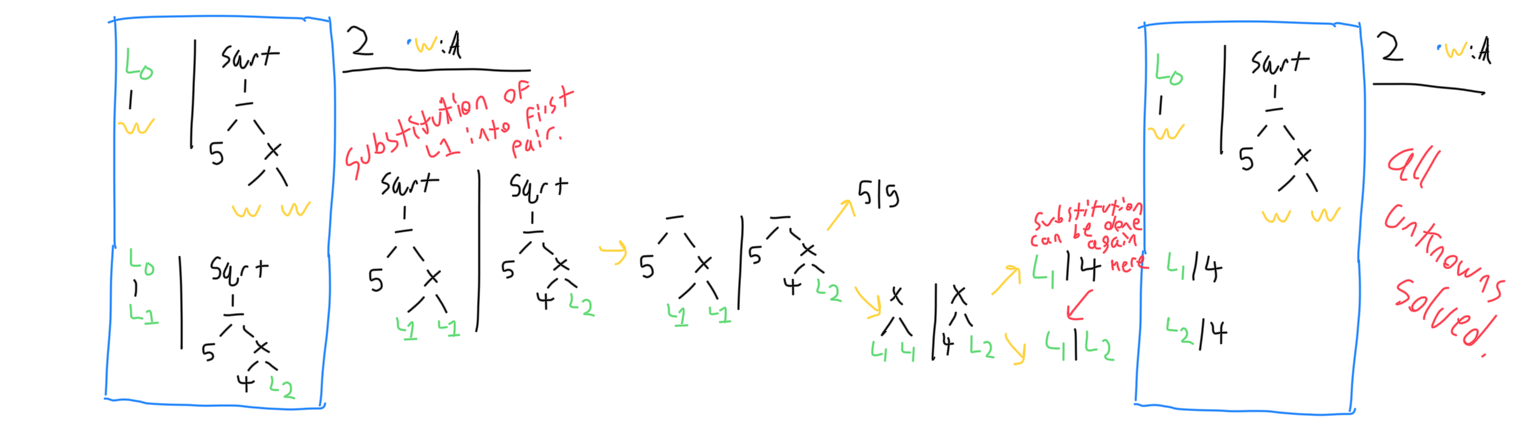
The second process is identifying which patterns can be substituted into other patterns. Substituting both sides of each pair and then going back to step one of the simplification process typically eliminates the target pair and creates more useful pairs from it.
In some cases, binding objects must be split into multiple different cases and simplified separately. The objective of this next algorithm is to handle cases like the one illustrated below, and turn them into more useful pairs. Essentially, the algorithm performs pattern matching and returns each possible combination.
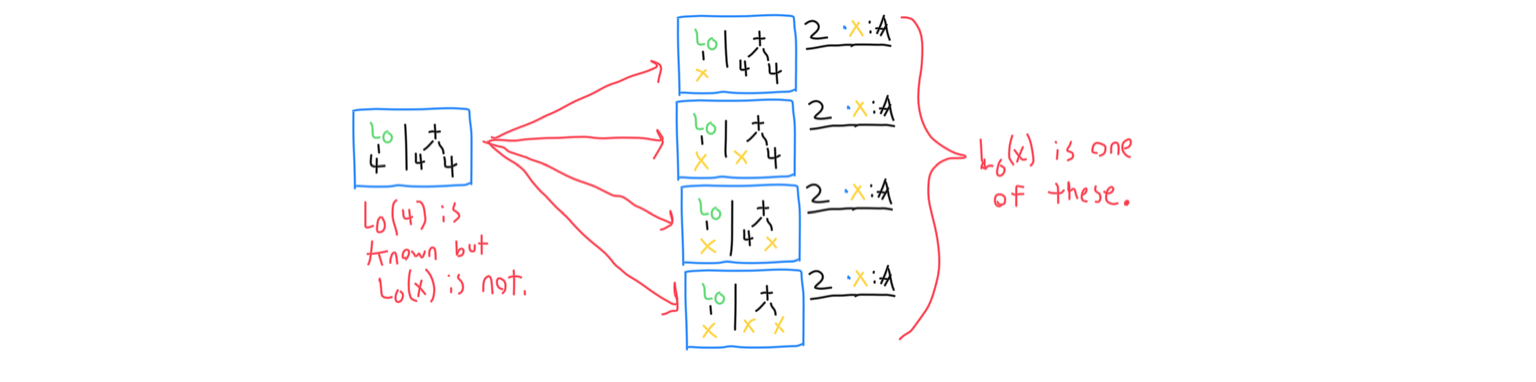
This problem is known as higher order unification. The next chapter focuses solely on it, because it can be a very difficult problem.